BatchNormalization and LayerNormalization
This post is to introduce Batch Normalization and Layer Normaliztion, which are of the $\textit{regularization}$ methods in $\textit{Deep Learning}$.
Regularization
Deep learning can be very powerful since the stacked deeper layers. Thus it’s easy to overfitt and has poor performance on unseen data. To avoid that, several regularization methods are been proposed. And this post will focus on two methods, namely $\textrm{Batch Normalization}$ and $\textrm{Layer Normalization}$.
Batch Normalization
Let’s assume that we want to train a fully connected neural network, and we add a batch normalization layer into the net. We insert it between the activation layer and input layer like follow figure.
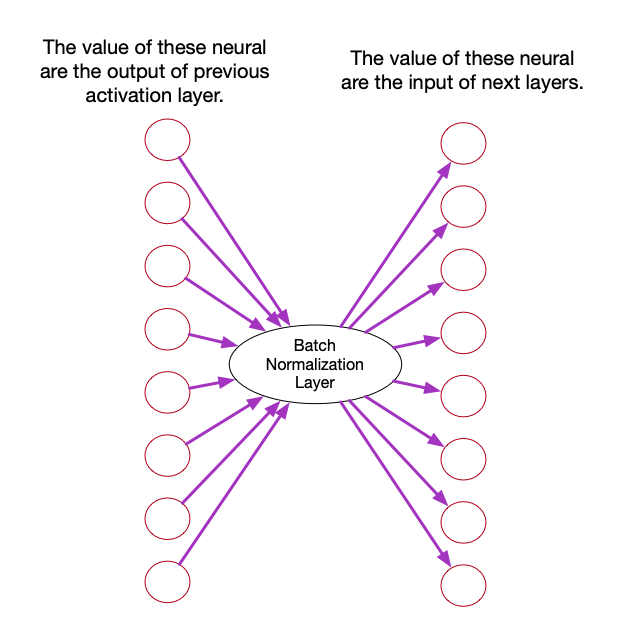
Firstly, we’ll discuss the train period.
As the name implies, we need to calculate mean value and standard variation value for each batch train data. Apparently, these two variables are vector. Assume previous layer has 100 neurons, then the mean and std are both 100 dimension.
The input shape of bacth normalization layer is (batch_size, 100), and use X to represent. So, when training with batch data, we do follow calculation in normalization layer for each batch. i is the number of batch, and the computation is element wise.
$$
X_i^{\prime} = \frac{X - \mu_i}{\sigma_i}
$$
After that, we use another two values $\gamma$ and $\beta$ to do another calculation. These two parameters are learnable, which means that they’ll be fitted with data in the training period like parameters W and b. The calculation is as follow:
$$
X_i^{\prime \prime} = \gamma X_i^{\prime} + \beta
$$
$X_i^{\prime \prime}$ will be sent to next layer doing $WX_i^{\prime \prime} + b$.
Now, how does batch normalization do during test period? There has no mean value and std for test data, since no batch. What we do is to use the $\mu_i$ and $\sigma_i$, which are calculated in batch train period time. Use these values to do weight average. Bigger the batch number is, higher the corresponding weight is.
Layer Normalization
Unlike batch normalization using each batch data to estimate $\mu$ and $\sigma$, layer normalization use the units of a layer. The mean value is the avearge of one layer’s units value, so as the standard variation. The equation is as follow:
$$
\mu_i = \frac{\sum_{j=1}^H a_H}{H} \\
$$
Other setting and steps are same as before.