Connectionist Temporal Classification

由于需要进行图片文本识别相关的工作，最近接触到了CTC Loss，打算将这几天的学习进行归纳总结。如果有接触过HMM的相关内容，看到CTC可能会觉得很亲切。

1. 前言

如果想要识别图片中的文字，神经网络是一个不错的选择，它们在大多数情况下表现良好。一般来说，用于文本识别工作的神经网络会用到convolutional layers和recurrent layers，前者常被用于提取图片中的特征并送入后者。后者的输出是一个矩阵，存放着每个时间步中属于某个字符的概率。基于CRNN架构的文字识别如下图所示，

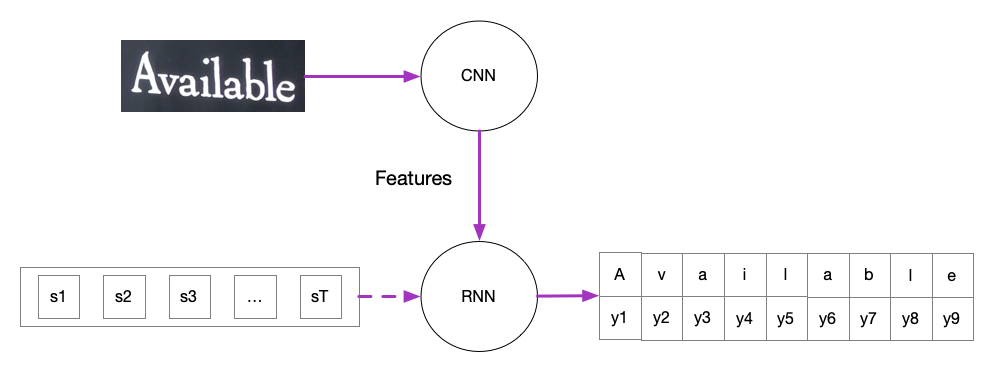
CRNN Overview

Figure1, CRNN Overview

要训练这样的网络，可以设想一下最通俗的做法，那就是字符级别的分类识别。比如对于上图来说，同时需要标注图片中每个字符的位置，比如图片中A所在的位置，然后这个部分对应的字符是A，依次类推，对这张图片里的其他字符还需要做同样标注行为。对于图片，这样标注仅仅只是耗时，但是有些任务比如语音识别，甚至无法标注字符出现的位置。

为了解决上述难题，CTC被提出了，它是一种能让RNN直接利用图片数据或语音数据与文本数据进行端到端训练的方法。

2. 对齐

不标注字符的具体位置，对于像图片数据转文字或者语音数据转文字的任务，会存在一个问题，那就是如何将输入与输出对齐。

拿图片来说，输入图片经过CNN后转化得到特征向量，将这些特征组成序列输入RNN。为了方便，RNN的序列步长T是固定的，相应的，RNN的输出也是T。但是，我们不能保证数据集<X, Y>中的文字长度都是T，RNN的输入与标签 y可能无法对齐。比如在图片Figure1中，设T = 10，而目标单词Available的长度只有9，此时就无法对齐。

为了解决对齐问题，为Figure1增加CTC Layer，加在RNN输出之后。

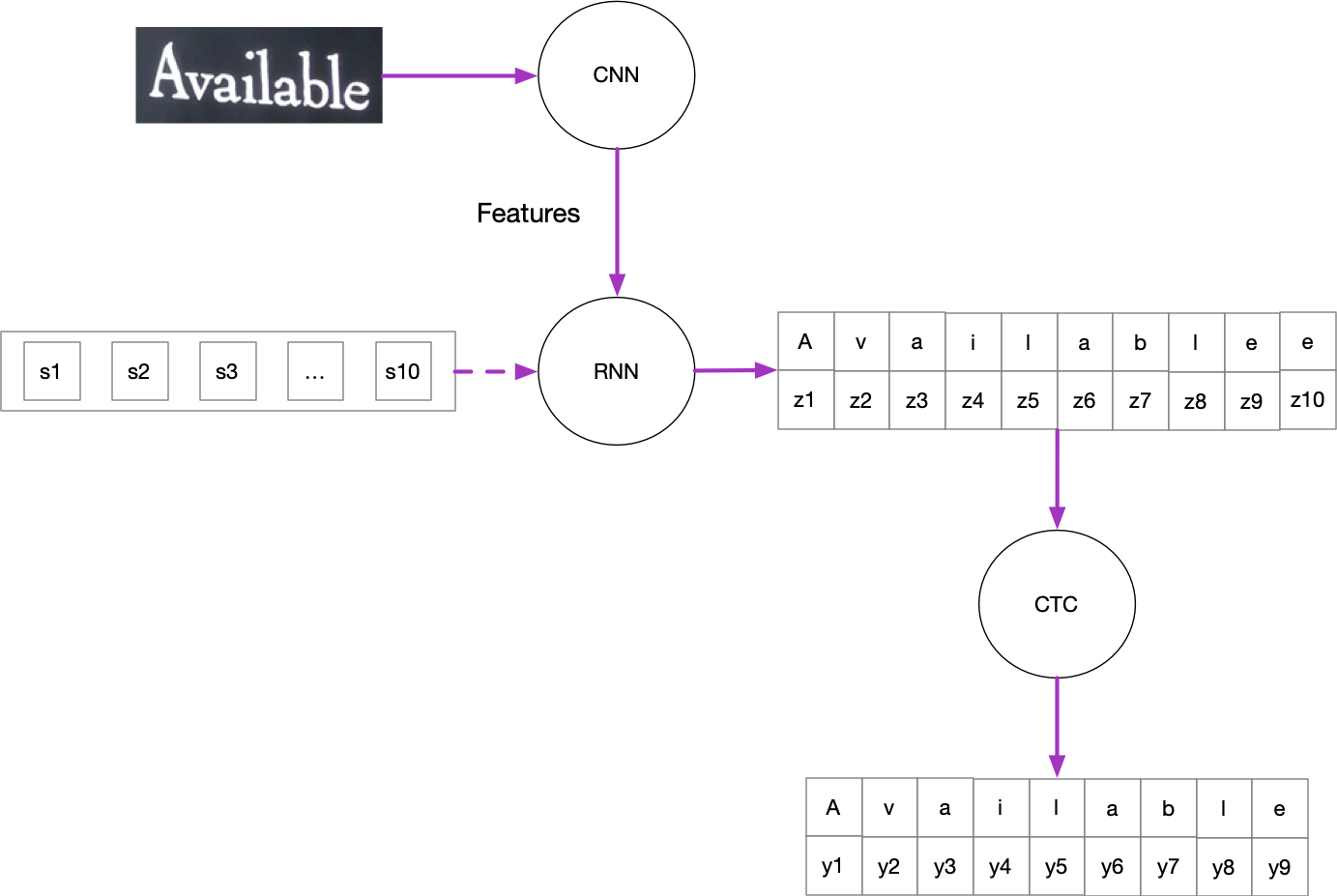
CRNN Overview

Figure2, CRNN with decoder

如Figure2所示，设RNN输出的步长固定为10。当$y_i$的长度不足10时，允许RNN能在相邻位置上预测出相同的字符。在CTC layer中解码时，将相邻相同的字符合并即可。

但是，又来了一个问题，如果$y_i == hello$，即标签中相邻位置本就存在相同字符，上述的解码策略就行不通了。为此，再引入一个特殊字符$\epsilon$，称作blank token，在解码的时候去掉。如果RNN序列长度还是10，那么比如RNN输出路径为$h e l \epsilon l \epsilon o o o o$，是能被解码到hello的。

总结来说，为了能够解决对齐问题，我们在RNN layer后加了CTC layer，并且为RNN的字符分类增加新的一类$\epsilon$。根据相应的解码规则，期待RNN的输出在经过CTC的转化后能得到正确路径。更加具体的解码细节，会放在第4部分概率计算中介绍。

3. 目标函数

终于来到本文的重点，这一部分将介绍CTC Loss。

到现在为止，我们知道RNN要处理的是多对多的多分类问题，它需要将输入的特征序列转化为序列矩阵。矩阵的每一行是字符所对应的类别，矩阵的每一列是所处的时间步。

3.1. 概率

为了更加形象，下面以具体的任务进行举例。假设待预测的图片只包括我爱学习4个字，RNN在每个时间步需要预测的字符也仅有5类$\{我，爱，学，习，\epsilon\}$，RNN的序列步长固定为5。那么RNN的一次输出可能产生如下矩阵：

	$step_1$	$step_2$	$step_3$	$step_4$	$step_5$
我	0.469	0.202	0.244	0.011	0.154
爱	0.043	0.217	0.211	0.314	0.185
学	0.249	0.179	0.207	0.152	0.204
习	0.144	0.13	0.137	0.296	0.227
$\epsilon$	0.096	0.272	0.2	0.227	0.231

每一个时间步，所有字符出现的概率和为1。下面，可以通过这个矩阵计算出解码层最后输出我爱学习的概率。首选需要列出所有可能解码出我爱学习的路径，但是值得一提的是，实际的解码过程中并不会通过这种穷举方法得到需要的概率，因为计算量非常的大。

路径：

$\epsilon$ -> 我 -> 爱 -> 学 -> 习
我 -> $\epsilon$ -> 爱 -> 学 -> 习
我 -> 爱 -> $\epsilon$ -> 学 -> 习
我 -> 爱 -> 学 -> $\epsilon$ -> 习
我 -> 爱 -> 学 -> 习 -> $\epsilon$
我 -> 我 -> 爱 -> 学 -> 习
我 -> 爱 -> 爱 -> 学 -> 习
我 -> 爱 -> 学 -> 学 -> 习
我 -> 爱 -> 学 -> 习 -> 习

上面列出了所有能得到正确解码序列的路径，共有9条。路径数量会受到RNN序列长度、标签文字长度以及标签文字中重复字符的个数的影响，而且是指数级别的增长。

接下来，需要分别计算上述路径的概率，之后再求和，即可得到模型输出我爱学习的概率。

\begin{equation}
\tag{1}
p(我爱学习|x) = \sum_{j=1}^{m=9} p(path^j|x) = \sum_{j=1}^{9} (\prod_{t=1}^5 p(z_t^j|x))
\end{equation}

3.2. 最大似然估计

参数的概率估计问题总是绕不过MLE。

前面已经以计算$p(我爱学习|x)$作为概率计算的举例。假定现在有一组数据集，包括$N$组图片与文字$\left<x_n, y_n\right>$的对应关系，记作$\left<X, Y\right>$。同样的，分别计算出这些样本产出的概率（再次强调，不会穷举计算，具体算法文章之后会介绍），得到若干组概率$p(y_n|x_n)$。

根据极大似然的思想，好的模型，或者说好模型的参数会令似然函数最大，希望根据下式得到模型的参数（为了书写简便$\theta$有时省略），有：

\begin{equation}
\tag{2}
\theta^* = \underset{\theta}{\mathrm{argmin}} \prod_{n=1}^N p(y_n|x_n, \theta)
\end{equation}

到这里，我们就得到了CTC Loss的目标函数(Objective function)，如下所示：

\begin{equation*}
\tag{3}
\label{a}
\max \prod_{n=1}^N p(y_n|x_n) \iff \max \sum_{n=1}^N \log p(y_n|x_n) \
\iff \min -\sum_{n=1}^N \log p(y_n|x_n)
\end{equation*}

如$\eqref{a}$式所示，目标是最小化negative log-likelihood。

4. 概率计算

在3.1中我们用穷举的方法列出了所有能得到文本我爱学习的可能路径，下面将介绍CTC的另一个核心部分，即如何优化概率计算算法。

CTC中用到概率计算算法与HMM的前向-后向算法很像，论文中称作CTC Forward-Backward Algorithm，下面以该称呼指代。前向-后向算法关注的点在于如何利用相邻时间步状态的关系简化计算量。

论文给出前向概率的定义如下：

\begin{equation}
\tag{4}\label{b}
p(y_1, y_2, \cdots, y_s|x) = \alpha_{t}(s) \stackrel{def}{=} \sum_{\pi \in N^{T}: \atop \mathcal{B}\left(\pi_{1:t}\right)=label_{1:s}} {} \prod_{t^{\prime}=1}^{t} y_{\pi_{t^{\prime}}}^{t^{\prime}}
\end{equation}

其中：

$\pi$是单条可能的路径，$N^{T}$是所有的路径，$T$是RNN的输入(输出)步长；
$\mathcal{B}$是解码的规则，就像前面说的那样，删除重复字符与去除blank token；
$t$代表路径中的第几个时间步，$s$代表标签的第几个字符。

总体来说，$\eqref{b}$看起来非常抽象，下面结合实际的标注文本：$我爱学习$

假定将RNN的输出步长$T$固定为10。现在需要计算第2个字符爱在时间步为5时的前向概率，那么可以写作$\alpha_{5}(\text{爱})$。为了更加清楚，在定义上加上字符的位置信息，写作$\alpha_{5}(label_2=\text{爱})$

此时，$label_{1:s}$就是$label_{1:2}$：$我爱$。我们需要找到所有的$\pi$，使得 $\mathcal{B}(\pi_{1:5}) == 我爱$。

比如，其中符合要求的路径$\pi$可以是：

$\epsilon \rightarrow \epsilon \rightarrow 我 \rightarrow \epsilon \rightarrow 爱 \rightarrow \cdots$
$\epsilon \rightarrow 我 \rightarrow 我 \rightarrow \epsilon \rightarrow 爱 \rightarrow \cdots$
$\epsilon \rightarrow 我 \rightarrow \epsilon \rightarrow 爱 \rightarrow 爱 \rightarrow \cdots$
$\cdots$

如上所示，虽然规定路径的长度为10，但由于需要的时间步$t$只有5，仅考虑前5个字符组合之后，符合解码需求的路径。

4.1. 前向算法

下面先用一张图来介绍前向过程中「字符的流动」。

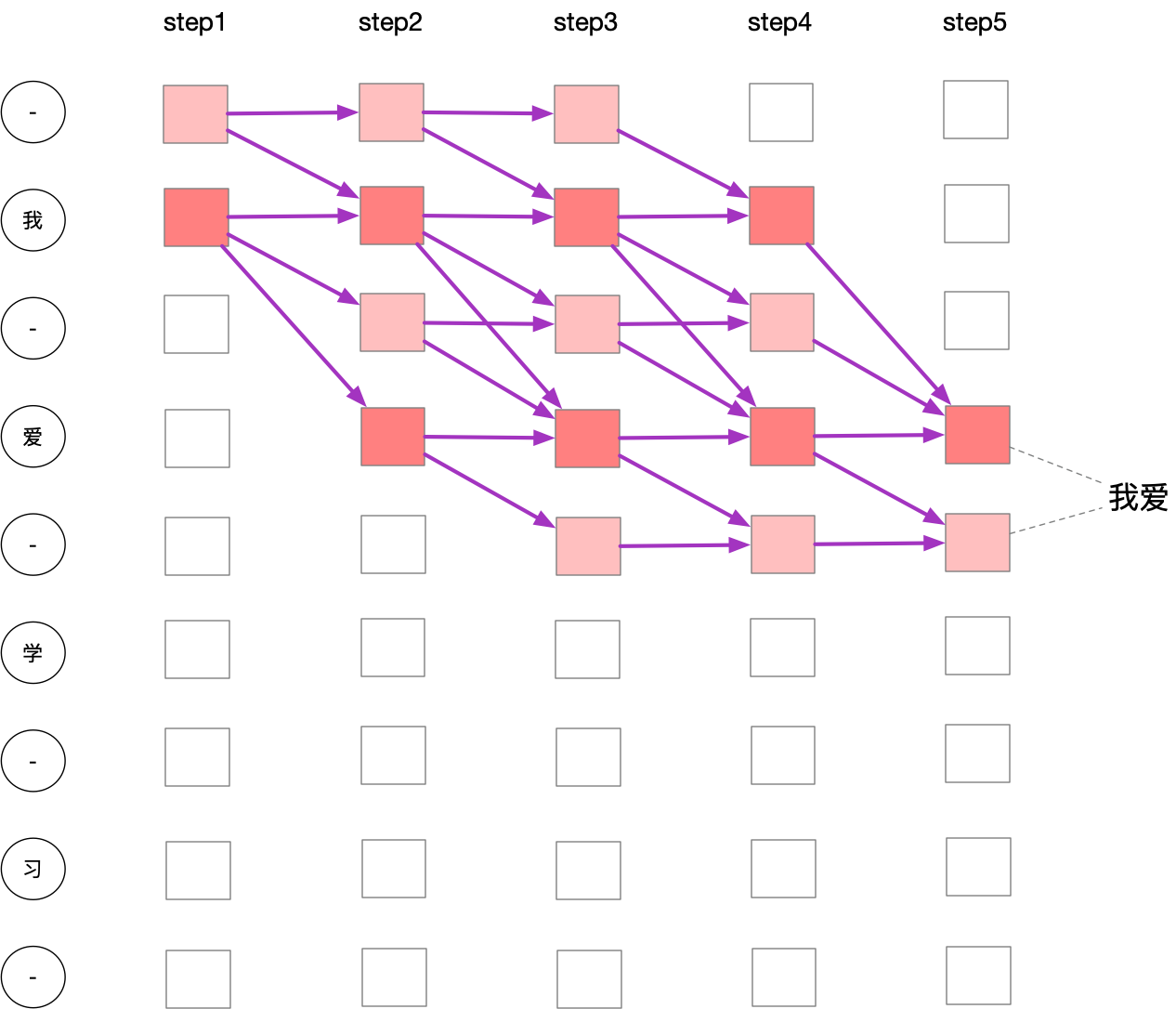
CTC Forward

Figure3, CTC Forward

需要注意的这张图并不是RNN的输出矩阵，实际的输出矩阵还是只有5行，「我，爱，学，习，$\epsilon$」。这里只是为了让前向过程的状态转变更好理解，所以做了添加$\epsilon$的操作。

$\epsilon$在图中用-表示。我们先是将$\epsilon$分别插入文本的头尾以及内部，然后从左上到右下，将所有可能得到$我爱$的路径画了出来。

为了契合上面的变化，对于文本也做相应的变化：$$label「我爱学习」\rightarrow label^{\prime} 「\epsilon我\epsilon爱\epsilon学\epsilon习\epsilon」$$

要获取$\alpha_{5}(label_2=\text{爱})$，可以利用公式(5)：

\begin{equation}
\tag{5}
\alpha_{5}(label_2=\text{爱}) = \alpha_{5}(label^{\prime}_ 4=\text{爱}) + \alpha_{5}(label^{\prime}_5=\epsilon)
\end{equation}

而，
\begin{equation}
\begin{aligned}
\alpha_{5}(label^{\prime}_ 4=\text{爱}) &= \left(\alpha_{4}(label^{\prime}_ 4=\text{爱}) + \alpha_{4}(label^{\prime}_ 3=\epsilon) + \alpha_{4}(label^{\prime}_ 2=\text{我})\right) * p(label^{\prime}=\text{爱}) \\
\alpha_{5}(label^{\prime}_ 5=\epsilon) &= \left(\alpha_{4}(label^{\prime}_ 5=\epsilon) + \alpha_{4}(label^{\prime}_ 4=\text{爱})\right) * p(label^{\prime}=\epsilon)
\end{aligned}
\end{equation}

当第$s$个$label^{\prime}$是$\epsilon$时，有两个转换来源；当是普通字符时，有三个转换来源。还有一个要注意的是，当相邻两个字符是相同的时候，也只有两个转换来源。如下图：

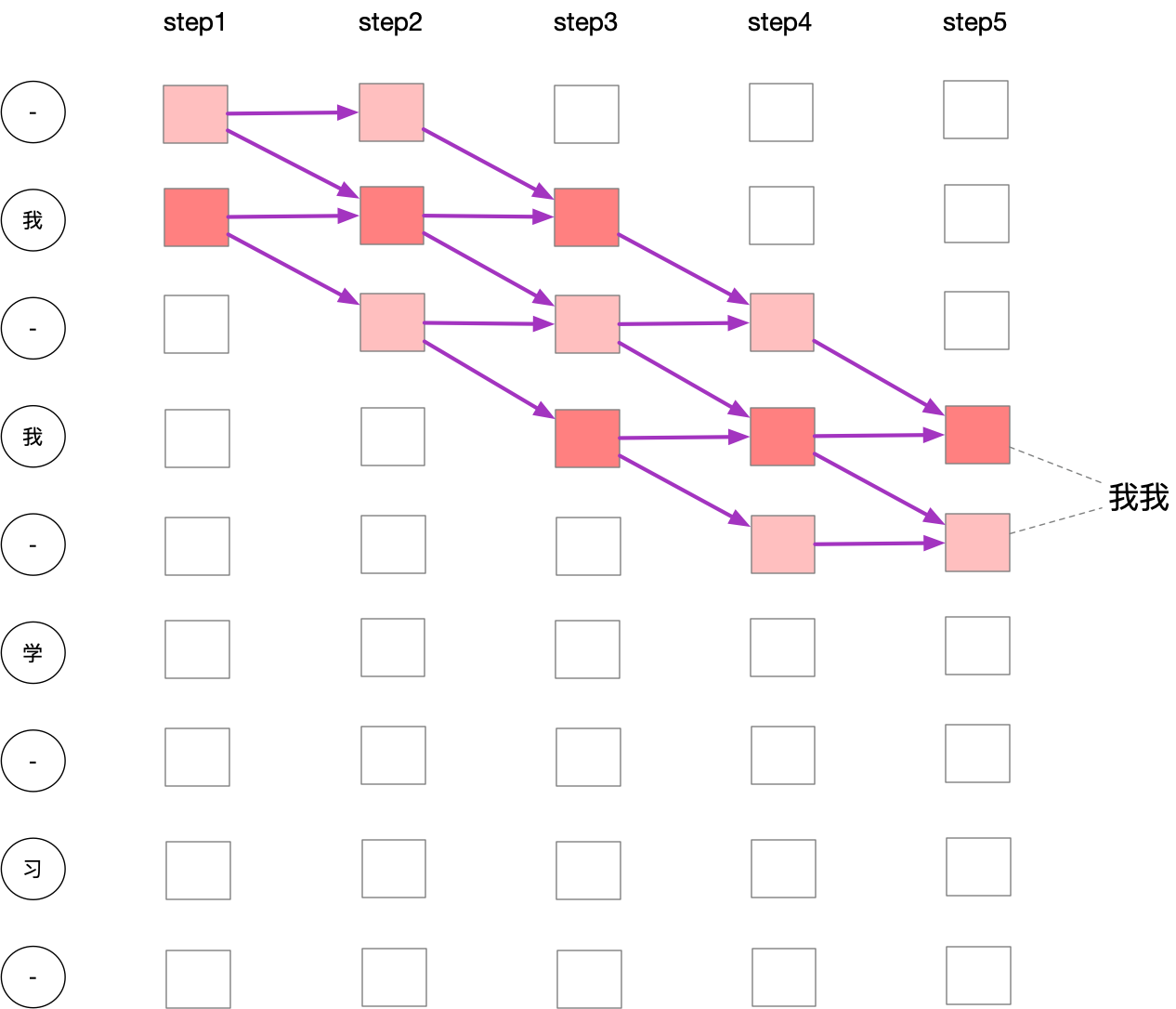
CTC Forward2

Figure4, CTC Forward 2

这样，我们可以写出针对$label^{\prime}$的转换方程，为了简写，用$l$代替$label$：

\begin{equation}
\alpha_t(l^{\prime}_s)=
\begin{cases}
\left[\alpha _{t-1}(l^{\prime}_s) + \alpha _{t-1}(l^{\prime} _{s-1})\right] * p(l^{\prime}_s), \ \ if \ \ l^{\prime}_s=\epsilon \ \ or \ \ l^{\prime}_s=l^{\prime} _{s-2}
\\
\\
\left[\alpha _{t-1}(l^{\prime}_s) + \alpha _{t-1}(l^{\prime} _{s-1}) + \alpha _{t-1}(l^{\prime} _{s-2})\right] * p(l^{\prime}_s), \ \ otherwise
\end{cases}
\end{equation}