在时序相关或者文本相关的任务中，人们常常会使用RNN-Based的序列模型，本文将主要介绍LSTM涉及到的一些知识点。主要参考几篇优秀的博文，链接将放在最后的Reference中，感兴趣的建议直接阅读原文🚘。

为了避免Vanilla RNN在输入长文本后带来的梯度消失问题，研究者提出了LSTM unit，即long-short term memory unit，使用它们作为整个序列模型中的最小单元。

在LSTM unit中共存在两种state，一类是hidden state，另一类是cell state。同时，引入了门机制，分别为Forget Gate、Update Gate/Input Gate以及Output Gate。在每一个time step时，模型通过上述的门机制决定应该存放哪些信息，同时过滤掉哪些信息。

首先，为了阐明LSTM unit的计算机制，先对其内部架构进行一定的了解，如下图所示：

LSTM unit

Fig 1. LSTM unit, from https://miro.medium.com/max/700/0*exoKHMF9vYA3ZJvJ.png

通过Fig 1，我们可以预览到LSTM传播时数据的大致流通过程。更近一步的，通过以下动图可以一目了然地观察到数据是怎么在一个unit中流动的。

Long Short Term Memory with its gates

Fig 2. Data flow in LSTM unit, from https://miro.medium.com/proxy/1*goJVQs-p9kgLODFNyhl9zA.gif

可以清晰地看到，在时间步t时，unit接收来自时间步t-1的$c_{t-1}$与$h_{t-1}$，经过若干次的线性变化以及point-wise操作后，输出c_t与h_t。下面将具体介绍每个门机制的运行过程以及个人对于该设计的理解。

首先，我们可以将内部计算中涉及到门计算的部分分为以下几种。

LSTM unit with gates

Fig 3. Three types of gates in LSTM unit, from https://miro.medium.com/max/700/0*G474BVfgtu5ZE4ai

其中：

  • 最左边的部分为Forget Gate;
  • 中间的部分为Input Gate或Update Gate;
  • 最右边的部分为Output Gate.

Forget Gate

对于上一个时间步传递的cell state信息，遗忘门决定哪些信息需要被继续保持，哪些信息应被遗忘。

假设当前所在的时间步为t，记当前forget gate的输入为$X_t$，$c_{t-1}$以及$h_{t-1}$，输出为$C_{tmp}$，根据上面动图中的计算，其相应的计算伪代码如下：

  1. 将$X_t$与$h_{t-1}$进行concatenation，得到$[h_{t-1}, X_{t}]$；
  2. 通过$W_{forget}$与$b_{forget}$进行线性转换，再通过sigmoid将计算结果转换到[0, 1]区间；
  3. 最后，将上述输出的概率向量与$c_{t-1}$中保存的向量做point-wise乘法。

下面是Forget Gate的计算公式：

  1. $Conbine = Concatenation(h_{t-1}, X_t)$
  2. $Z_f = Sigmoid(W_{forget} Conbine + b_{forget})$
  3. $c_{tmp} = c_{t-1} * Z_f$

通过Forget Gate的一系列操作，上一个时间步的$c_{t-1}$第一次得到了更新，得到了$c_{tmp}$。我们用它表示在时间步t输出最终cell state前的中间值。

我认为遗忘门运作的机制是：将之前保存的信息（存放在$h_{t-1}$）与当前时间步的输入信息（$X_t$）进行比较，进而去判断是否对$c_{t-1}$中的某些信息进行遗忘。当sigmoid输出的向量中某个位置输出的概率值更偏向于0，则说明$c_{t-1}$对应位置上的信息应该被遗忘；而当该位置的概率值更偏向1时，则$c_{t-1}$对应位置上的信息更应该保留。

Update Gate/Input Gate

更新门需要考虑将哪些新信息保存或者贴加到cell state中，并且输出到下一个时间步。

在Update Gate中，unit决定什么信息要被更新到$c_{tmp}$中。这组门运算的输入包括：$h_{t-1}, X_t, c_{tmp}$，输出为$c_{t}$：

  1. 第一步还是同Forget Gate中形式的一样，先将$X_t$与$h_{t-1}$进行concatenation，得到$[h_{t-1}, X_{t}]$；
  2. 接下来，分别进行两次线性变换，但是各自activation function不同，一个为sigmod，而另一个则为tanh；
  3. 最后，将两个结果进行point-wise的乘法，得到Update Gate的输出。

同样的，下面是Update Gate的计算公式：

  1. $Conbine = Concatenation(h_{t-1}, X_t)$
  2. $Z_u = Sigmoid(W_{update1} Conbine + b_{update1})$
  3. $O_u = Tanh(W_{update2} Conbine + b_{update2})$
  4. $c_{t} = c_{tmp} + Z_u * O_u$

更新门中共存在两组线性转化的参数：$(W_{update1}, b_{update1})$以及$(W_{update2}, b_{update2})$，各自的结果转化之后相乘，再加到$c_{tmp}$上，最后得到当前时间步将要输出的cell state。

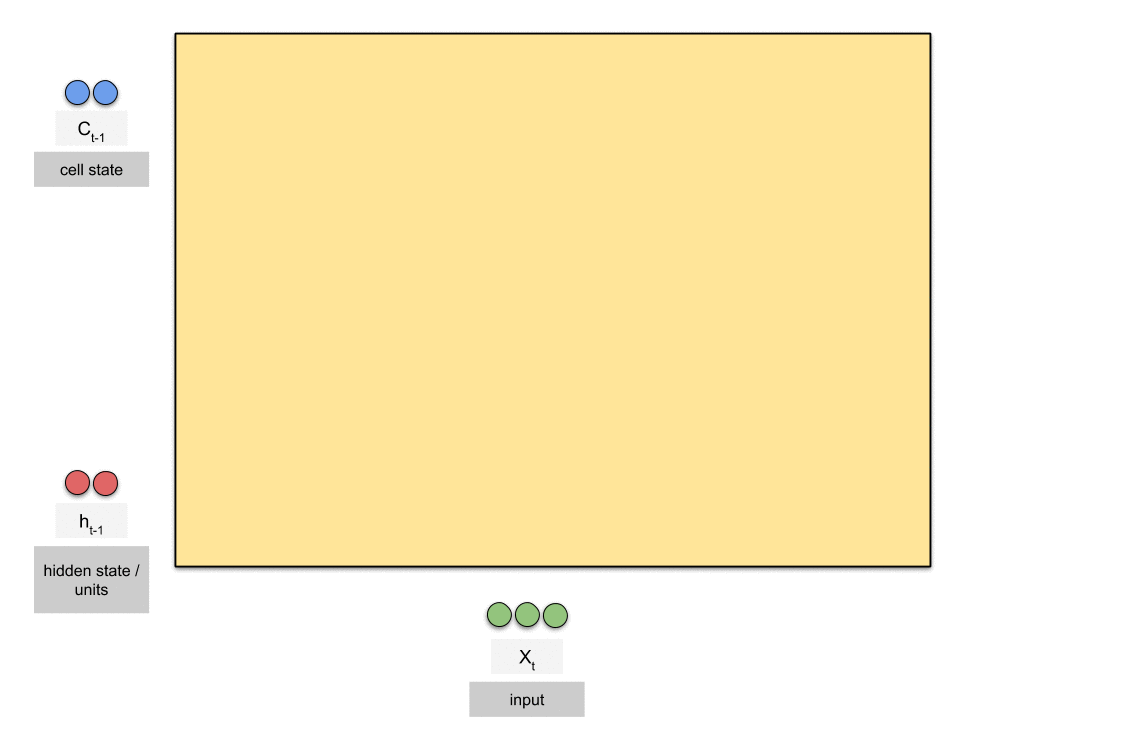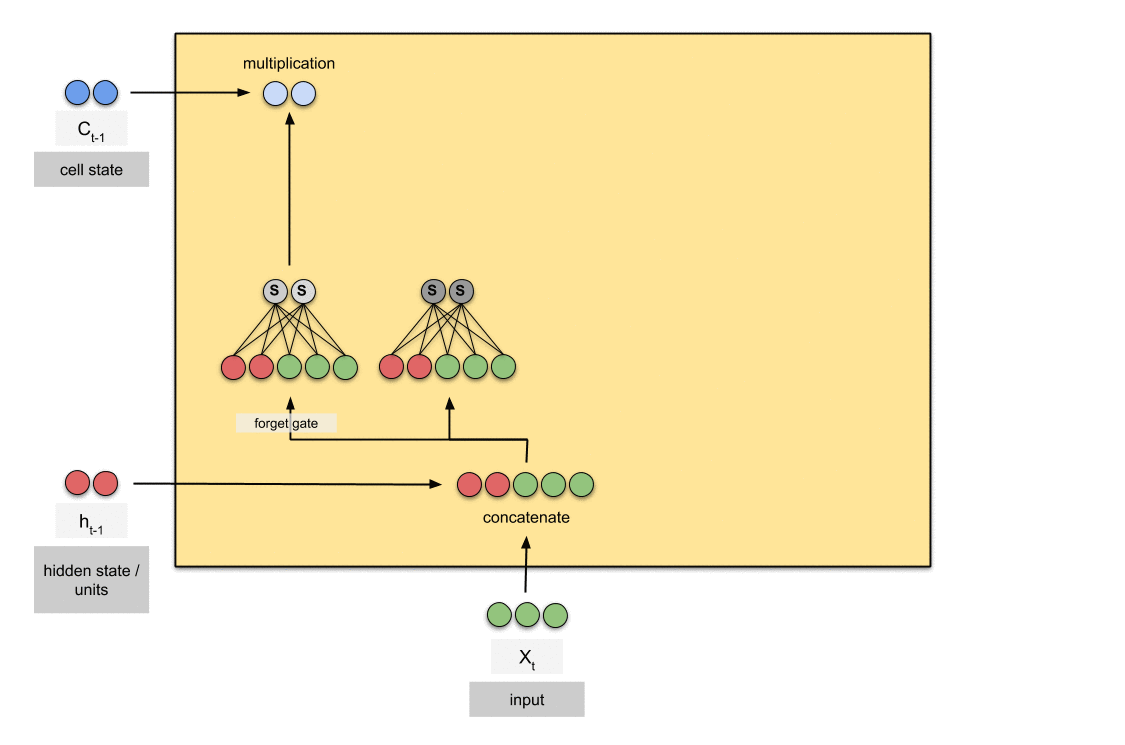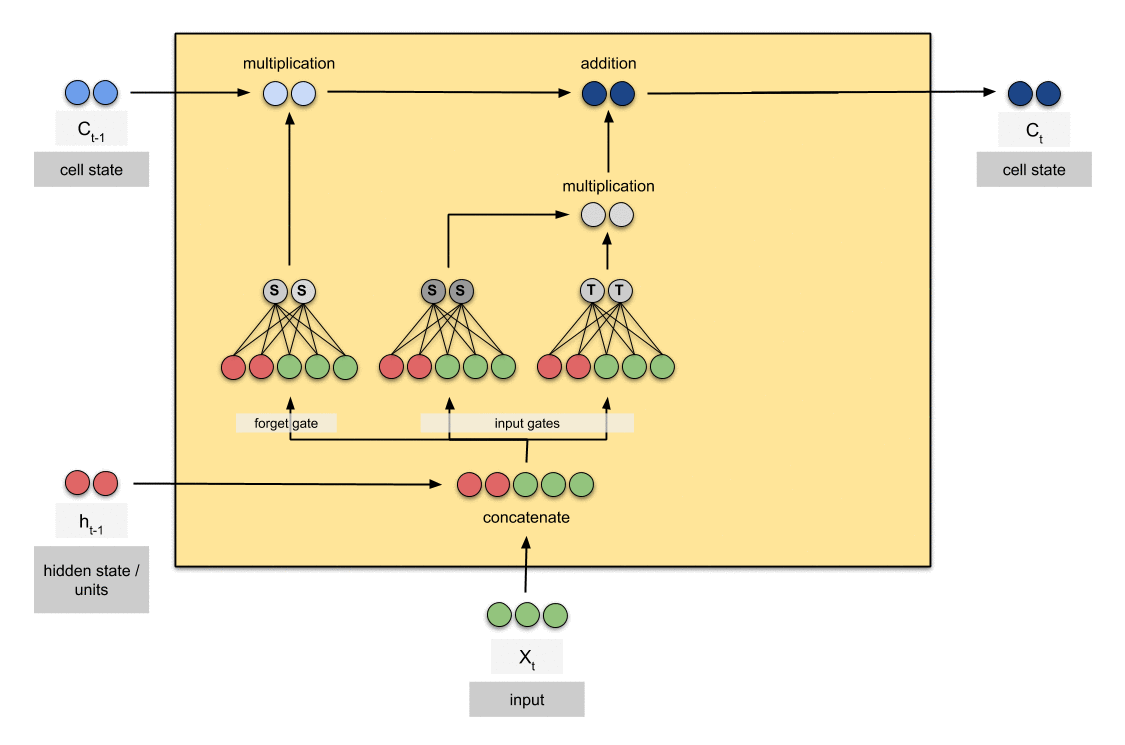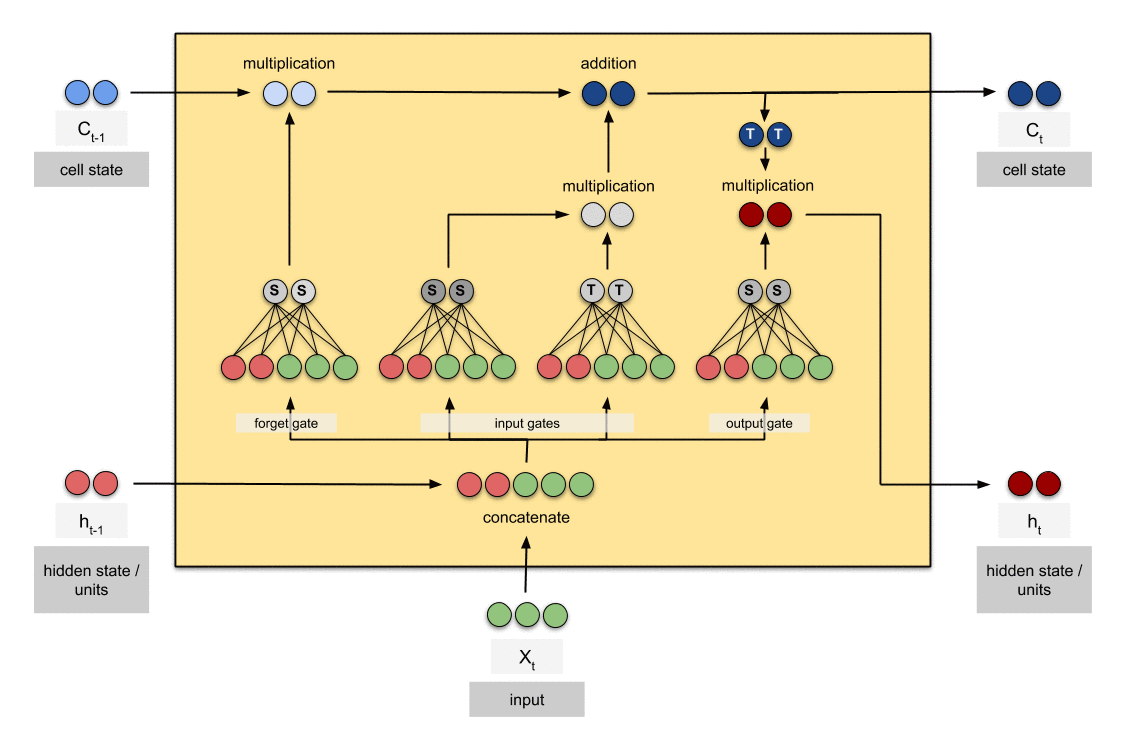
Output Gate

输出门的作用在于结合各种信息，在当前的时间步做出决策，同时为下一个时间步的计算提供信息。

除去上述的两组，unit中还剩下一组门运算，即输出门。它的输入包括$h_{t-1}, X_t, c_{t}$，最后的输出为$h_t$:

  1. 第一步依旧是拼接$X_t$与$h_{t-1}$，得到$[h_{t-1}, X_{t}]$；
  2. 通过$W_{output}$与$b_{output}$进行线性转换，再通过sigmoid将计算结果转换到[0, 1]区间；
  3. 将$c_t$通过tanh运算；
  4. 最后将2、3步的输出做point-wise的乘法，得到Output Gate的输出，也就是$h_t$。

同样，下面是Output Gate的计算公式：

  1. $Conbine = Concatenation(h_{t-1}, X_t)$
  2. $Z_o = Sigmoid(W_{output} Conbine + b_{output})$
  3. $O_o = Tanh(c_t)$
  4. $h_t = Z_o * O_o$

总结

到此，一个LSTM unit中的计算流程已经走完，下面我想谈一下个人对于其中几点的理解。首先是出现了两种激活函数sigmoid以及tanh。其中，sigmoid共出现了3次，分别在三个门中都出现；tanh则是出现在Update Gate以及Output Gate中。

sigmoid能将数值缩放至[0, 1]区间，它在LSTM unit中的使用都是与其他向量做point-wise的乘法，所以我认为使用它主要是为了使unit在处理时能够将信息进行保存或者遗忘。

tanh能将数值缩放至[-1, 1]区间，它在LSTM unit中被使用时基本上是为了将信息转化为数值，在Update Gate中，该数值会被记录到cell state中，在Output Gate中，该数值会被转化为下一个时间步的hidden state。

Reference