LoRA Explained

近些时间，大模型如雨后春笋般，突的一下，进入公众视野，诸如语言领域的ChatGPT，或是图像领域的Stable Diffusion。它们在各自领域上带给用户不俗的使用体验。在算法应用开发的角度，我们更关心能不能在特定的算法环境中使用上这些先进的大模型，而庞大的模型参数量为这个问题蒙上一些不确定性。本文要介绍的LoRA无疑是为大模型的训练提供了一种新的可能。

近些时间，大模型如雨后春笋般，突的一下，进入公众视野，诸如语言领域的ChatGPT，或是图像领域的Stable Diffusion。它们在各自领域上带给用户不俗的使用体验。同时，也不禁令人思考，AIGC到底能再往前进化到何种程度？

在ChatGPT如日中天，鼎沸到在食堂排队都能听到其他同事乐此不疲地讨论时，我对它的“落地”并不抱有期待。因为在算法应用开发的角度，我们更关心能不能在特定的算法环境中使用上这些先进的大模型，而庞大的模型参数量为这个问题蒙上一些不确定性。

Background

LLM Parameters

公司	模型	参数量（Bilion）	计算资源
OpenAI	GPT-3	175	30000+ A100
Google	PaLM-E	562	/
Meta	LLaMA	7/13/33/65	2048 A100 for 5 months

注：bert-base的参数量是110 milion

基于拥有如此庞大参数量的大模型，在进行下游任务的fine-tuning时，更新LLM的全部参数需要大量的计算资源。

What’s LoRA

LoRA，即low-rank adapation的缩写，它是一种应用在LLM fine-tuning阶段的训练方式。它能帮助以较少的计算资源和开销进行LLM fine-tuning，比较知名的项目有：

基于LoRA fine-tuning的模型性能没有过多降低。在论文的实验部分，甚至还有一些任务反超了fully fine-tuned model。

Adding adapater layers

该类方法的主要思想就是在大模型中新增一些adapter layers，在fine-tuning过程中，仅更新这些新增的参数，避免对大模型整体参数的更新，以达到降低计算开销的目的。以下为部分工作：

严格来说，LoRA也属于这种方式，但是相比于上述工作，它在推理时的速度并不会因为新增的参数而降低，后续会详细介绍它的计算方式。

Optimizing the input word embedding

比较新颖的方法，Prefix-Tuning旨在Embedding Layer增加额外参数，冻结剩余网络参数，以进行下游任务的训练。

2021，Prefix-Tuning: Optimizing Continuous Prompts for Generation

LoRA Method

Intrinsic Dimension

Swiss roll data

Swiss roll data curves, from https://twitter.com/lightonio/status/1240687522608373760

From Wikipidia

The intrinsic dimension for a data set can be thought of as the number of variables needed in a minimal representation of the data.

Fine-tune LLM

我们都知道，有监督神经网络的训练范式大多基于梯度下降，即一轮batch data过后，通过本轮数据计算loss更新网络参数$W$。假定当前轮为第$t$，即：

$$
\begin{equation}
W_{t+1} = W_t - lr * \Delta{W_t}
\end{equation}
$$
对于模型的训练，其本质是参数$W$的不断更新，记初始参数为$W_0$，训练结束得到的参数为$W_T$。对于LLM来说，$W_0$代表作为Pretrained-model的参数，通过多轮的训练，经历多个$\Delta{W}$的更新后得到$W_T$。在更新的过程中，有：

$$
\begin{equation}
\begin{gathered}
W_1 = W_0 - lr * \Delta{W_0} \\
W_2 = W_1 - lr * \Delta{W_1} \\
W_3 = W_2 - lr * \Delta{W_2} \\
\ldots \\
W_T = W_{T-1} - lr * \Delta{W_{T-1}}
\end{gathered}
\iff
W_T = W_0 - lr * (\Delta{W_0} + \Delta{W_1} + \cdots + \Delta{W_{T-1}})
\end{equation}
$$

从这个角度来看，对模型fine-tuning的过程就像是学习一个适应特定任务的$\Delta{W}$，结合$W_0$及$\Delta{W}$进行推理，如图1所示。因此，若将$\Delta{W}$作为可训练的参数，fine-tuning LLM即转化为对$\Delta{W}$的拟合。

图1

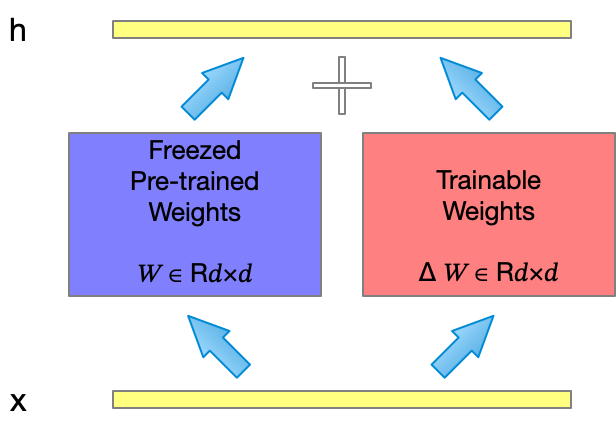
Introduce LoRA

有论文在实验对比的过程中，发现LLM的参数有着较低的$\text{Intrinsic Demension}$，受此启发，LoRA的作者假定$\Delta{W}$也存在这种特性。

From LoRA Paper

Inspired by this, we hypothesize the updates to the weights also have a low “intrinsic rank” during adapation.

若$\Delta{W}$存在较低的$\text{Intrinsic Rank}$，可以对其进行矩阵分解$\left(\text{Matrix Factorization}\right)$，即：
$$
\begin{equation}
\Delta{W} = BA
\end{equation}
$$

$\Delta{W} \in \mathbb{R^{d*k}}, B \in \mathbb{R^{d*r}}, A \in \mathbb{R^{r*k}}, r \ll \min(d, k)$，使用$(3)$式表示$\Delta{W}$之后，参与学习的参数量得倒缩减，由$O(d * k)$缩减至$O((d + k) * r)$。

图2

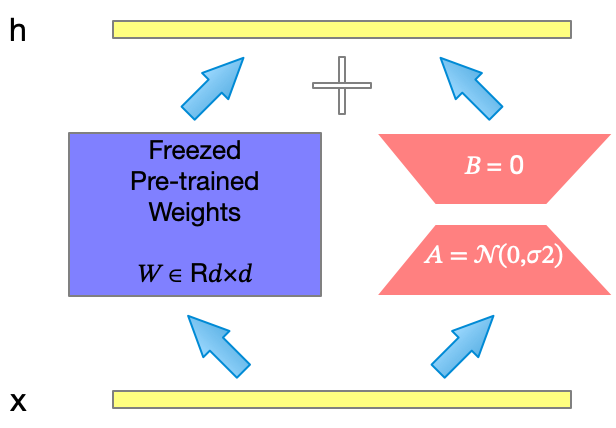
Practice

LoRA的想法看起来十分简单，目前开源社区有两方实现其工程代码。

后者主要对在PyTorch FSDP的训练模式上进行调整，但在使用形式上没有区别，以下基于论文作者的版本进行介绍。

Quick Start

安装

pip install git+https://github.com/microsoft/LoRA

使用

创建

# ===== Before =====
layer = nn.Linear(in_features, out_features)

# ===== After ======
import loralib as lora
# Add a pair of low-rank adaptation matrices with rank r=16
layer = lora.Linear(in_features, out_features, r=16)

循环

import loralib as lora
model = BigModel()
# This sets requires_grad to False for all parameters without the string "lora_" in their names
lora.mark_only_lora_as_trainable(model)
# Training loop
for batch in dataloader:
   ...

保存模型

# ===== Before =====
torch.save(model.state_dict(), checkpoint_path)
# ===== After =====
torch.save(lora.lora_state_dict(model), checkpoint_path)

LoRA Layer

class LoRALayer:
    def __init__(
        self, 
        r: int, 
        lora_alpha: int, 
        lora_dropout: float,
        merge_weights: bool,
    ):
        self.r = r
        self.lora_alpha = lora_alpha
        # Optional dropout
        if lora_dropout > 0.:
            self.lora_dropout = nn.Dropout(p=lora_dropout)
        else:
            self.lora_dropout = lambda x: x
        # Mark the weight as unmerged
        self.merged = False
        self.merge_weights = merge_weights

class Linear(nn.Linear, LoRALayer):
    # LoRA implemented in a dense layer
    def __init__(
        self, 
        in_features: int, 
        out_features: int, 
        r: int = 0, 
        lora_alpha: int = 1, 
        lora_dropout: float = 0.,
        fan_in_fan_out: bool = False, # Set this to True if the layer to replace stores weight like (fan_in, fan_out)
        merge_weights: bool = True,
        **kwargs
    ):
        nn.Linear.__init__(self, in_features, out_features, **kwargs)
        LoRALayer.__init__(self, r=r, lora_alpha=lora_alpha, lora_dropout=lora_dropout,
                           merge_weights=merge_weights)

        self.fan_in_fan_out = fan_in_fan_out
        # Actual trainable parameters
        if r > 0:
            self.lora_A = nn.Parameter(self.weight.new_zeros((r, in_features)))
            self.lora_B = nn.Parameter(self.weight.new_zeros((out_features, r)))
            self.scaling = self.lora_alpha / self.r
            # Freezing the pre-trained weight matrix
            self.weight.requires_grad = False
        self.reset_parameters()
        if fan_in_fan_out:
            self.weight.data = self.weight.data.T

    def reset_parameters(self):
        nn.Linear.reset_parameters(self)
        if hasattr(self, 'lora_A'):
            # initialize A the same way as the default for nn.Linear and B to zero
            nn.init.kaiming_uniform_(self.lora_A, a=math.sqrt(5))
            nn.init.zeros_(self.lora_B)

    def train(self, mode: bool = True):
        def T(w):
            return w.T if self.fan_in_fan_out else w
        nn.Linear.train(self, mode)
        if self.merge_weights and self.merged:
            # Make sure that the weights are not merged
            if self.r > 0:
                self.weight.data -= T(self.lora_B @ self.lora_A) * self.scaling
            self.merged = False
    
    def eval(self):
        def T(w):
            return w.T if self.fan_in_fan_out else w
        nn.Linear.eval(self)
        if self.merge_weights and not self.merged:
            # Merge the weights and mark it
            if self.r > 0:
                self.weight.data += T(self.lora_B @ self.lora_A) * self.scaling
            self.merged = True

    def forward(self, x: torch.Tensor):
        def T(w):
            return w.T if self.fan_in_fan_out else w
        if self.r > 0 and not self.merged:
            result = F.linear(x, T(self.weight), bias=self.bias)
            if self.r > 0:
                result += (self.lora_dropout(x) @ self.lora_A.T @ self.lora_B.T) * self.scaling
            return result
        else:
            return F.linear(x, T(self.weight), bias=self.bias)